If you are reading this, there is a good chance you were aware of the level of intensity this year’s pi day brought. On Saturday, 3/14/15 at 9:26 nerds around the world celebrated and reflected on the beauty that comes from dividing any circle’s circumference by its diameter. It makes sense, then, that I began 8th hour on Friday asking my students “So are you guys excited for tomorrow?!” Little did I know, that question would help transform the next 45 minutes of class into one of the best lessons I have ever been a part of.
Let me start by mentioning this 8th hour class is a smaller class filled with students that have struggled with math for one reason or another. I’ve got freshman, sophomores, juniors, and seniors coming from Algebra 1, Geometry, and Algebra 2. They are not used to having quality conversations about math. In fact, just the opposite – I actually planned on them continuing their online course work silently.
Here’s what happened when I winged a class period
Part One – The Set Up
Teacher: Are you excited about tomorrow?!
Student 1: You mean Pi Day?
T: Yeah! Pi Day because 3/14/15 (I write it out). At 9:26 it’s gonna be the bomb!
Student 2: How many digits of pi do you know?
T: Let me show you something! (I walk over to my computer)
Student 3: Can we not do anything today?
T: Just one thing – then we can do whatever. (Bring up my email to show them this banter between some staff members)
At this point the students laugh, call me a geek – whatever. Then one student goes – isn’t it 3.141…and has like 13 digits memorized! A student I normally have to bargain with to get any work done knows 13 digits! How cool!
Part Two – Intro to Pi
T: Okay, let’s watch this quick video on pi, then I’ll stop with the nerdy stuff. (I show them this awesome Jo Boaler material)
T: Okay, so C = d* pi right? Does anyone remember the formula for area of a circle?
S1: Isn’t it pi*r^2?
T: Yes! It is. How do you know that?
S1: I don’t know… it’s what we learned.
T: Okay, well how can we show it? (I draw the picture to the right)
S2: That’s a nice circle.
T: So in the circle the radius is always the same length all the way around. We’ve got r and r so that makes this box the area of…
S1: r squared.
T: Nice! How do you know that?
S1: Because it’s r times r.
T: Okay, so how does r squared relate to A = (pi * r^2)? Why does that make sense as a formula?
Silence
T: Okay. How many of these boxes do you think fit in the circle? (pointing to the r squared box)
S1: 3.14. You know it’s going to be less than 4. You have to cut the edges off.
T: Good. So you have 3.14 of them right? pi *r^2? Alright, bare with me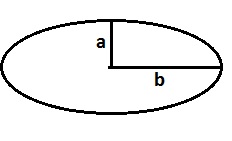 
(as I draw the ellipse to the right). Just one more thing. (20 mins of class left at this point). What is this shape?
S2: An oval.
T: Yeah, as you get higher in math we call it an ellipse. That’s not important. What I want you to see is that here we have this “a” and this “b”. What do you think the formula is for the area of an ellipse?
Blank stares
Part Three – Setting Up The Conversation
At this point I take time to lecture students on the process of turning on their brains. They have never been asked to think and participate in a discussion where the formula hadn’t already been given to them. “It’s okay to be wrong! We know our brains grow more when we make mistakes, but you have to try!”
S3: But when I raise my hand and get the answer wrong people will laugh at how wrong I am.
T: Exactly! That’s terrible, but realize that’s not you; it’s the environment your teacher has allowed. I doubt they even realize it, so it’s on all of you to be comfortable being wrong. Let me ask you…how many students tend to answer questions in class?
S4: 2 or 3.
T: That’s a problem. A teacher often needs to go off of their gut feeling. If you only let those 2 or 3 people answer the teacher will believe that everyone is good! You need to be okay with being wrong. Now I want you all to really think!
S1: Would it be pi * (a*b)?
T: Why?
S1: Because its pi * r * r. Why not make it pi * a * b?
T: What would that look like in a picture? How could we use area to explain your idea?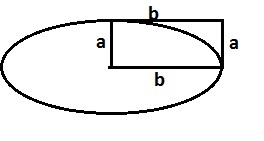
S1: Draw a box.
T: Okay what’s the area of this box? (students start with their thoughts)
ab^2
a^2*b^2 <= these were the three options that were thrown out by students
ab
I then ask each student to explain their explanation.
S4: (a^2 * b^2) Well I know there are two a’s and two b’s and I know it’s multiplying because of the r squared thing.
S3: (ab^2) That’s what I said for my formula two.
T: Are they the same thing then?
S5: They need to have parentheses so the exponent goes to both.
T: (I draw in parentheses with arrows showing the exponent effecting both the a and the b) Do we understand the difference? (They do!)
S5: (ab). So I just figured before we only had an r and an r so we would only need an a and b, not two of each.
S4: No way! Can’t you see my answer is right. Mr. Ulrich even just showed the thing with the two!
S5: But the r square would be r and r on the opposite sides and we didn’t use two of them.
The argument went on for about a minute – a few other students chimed in and soon enough we voted. After all arguments were given the class landed on the formula a^2 * b^2.
So what’s the answer?! – They ask.
T: Well…you’re all wrong. (groans) But, you were thinking and debating and that’s what is important in learning. You made a mistake, yes, but you learned and used your brains!
With only about six minutes of class left I tied our findings to pi, recapping that there is 3.14 of those rectangles in an ellipse and… boom – an amazing lesson with two minutes left to spare.
Let’s recap what was covered
- how many digits of pi are there?
- what does pi represent?
- formula for circumference of a circle
- formula for area of a circle and ellipse
- why mistakes are important to make
Math practices used
- Make sense of problems and persevere in solving them
- Construct viable arguments and critique the reasoning of others